Google OR Tool解路径规划

发表于 |

这是一个号称Google官方的开源优化sdk， 包括建模框架，CP求解器，支持市面上主流求解器，同时自带部分算法。这套框架已经上线好几年了，一直没有机会尝试。这次就实现一个简单的CVRP(Capacitated Vehicle Routing Problem， 运力约束的车辆路径规划)来测试一下。之后会将尝试VRPTW/MDCVRPTW等更加实际的模型。 该sdk目前最大的风险是只有一个人在维护。作者Laurent Perron是Google Paris的员工，而之前11年则一直在ILOG工作，2008年离职！ 要知道2008年IBM收购了著名的ILOG，许多ILOG的精英大佬不满IBM的收购成批出逃。一部分不甘认输另起炉灶，创立Gurobi和IBM分庭抗礼。而这帮精英大佬也确实说到做到，短短几年就让Gurobi声名鹊起，现在已经稳稳压IBM CPLEX一头。 而这位大哥则选择投奔Google，凭一人之力，弄出了这套sdk。可见当年合并前的ILOG，技术实力恐怖如斯！

简介

该套件包括以下内容

  • constraint programming solver
  • 支持主流求解器(CBC, CLP, GLOP, GLPK, Gurobi, Cplex, SCIP)
  • 各种网络算法: 最短路径(shortest path)，最大流(max flow), 最小费用流（min cost flow）
  • 旅行商问题TSP(traveling salesman problem), 路径规划问题VRP(vehicle routing problem)
  • 部分动态规划算法

其中最大的亮点在于能求解VRP。 在OR-tool的范例中，不但给出了VRP的例子，还给了一个VRPTW（vehicle routing problem with time window）的例子。 这就很厉害了，市面上针对VRP的成熟sovler凤毛麟角。 可在共享经济，新零售和无人驾驶的狂潮之下，VRP的应用场景实在太多了，比如共享送货， 接N个单的共享专车，等等。

安装

官方教程简单明了，使用pip安装十分容易。很可惜，目前or-tool还不支持conda。

1
sudo pip install ortools

之前提到or-tool的开发人员实际只有一人， 实在精力有限。 开发论坛里15年就有人提出建议，希望能加入conda安装。Laurent给出的理由是：没有时间。 也是艰难的很。

案例

我手头上正好有一个共享送菜案例的订单记录， 不妨用这个小数据集作为一个案例。该数据包含300+客户和一个货站。为了简化问题，这里不考虑运力，时间等约束，只对路径进行优化。 好了，下面是小xuo生应用题时间， 题目如下：
有一家货运公司，需要给300+个客户需要送货,假设客户均只送一件。 公司现有小货车10辆， 每辆能装载35件货物。 公司王经理负责为车队设计送货路线， 为保证司机师傅安全驾驶，每条线路总里程不能超过50公里。每条线路从货站(index = 0)出发， 最终返回货站。 王经理希望在满足以上条件的情况下，总里程最短。 请问王经理该如何实现？

模型

客户的位置的经纬度已经得到，格式如下：

id due_at latitude longitude
240254 2014-03-13 17:00:00 37.7819410348 -122.398127254
240368 2014-03-13 18:00:00 37.7861609629 -122.399636312
240369 2014-03-13 18:00:00 37.7789823487 -122.407610425

货站只有一个，所有货运路径必须从货站出发，最后回到货站。 数据中也给出最晚的送达时间due_at,留作以后扩展到VRPTW的时候使用。在这篇文章中只考虑VRP问题。 每辆车装载量是35件，每个客户只送一件， 即意味着每条线路最多拜访35个客户。 司机师傅只能开50公里， 那么每条线路的总距离是50.
因此该问题可以描述为：

  • 目标函数： 总路径最短
  • 约束1 - 距离约束： 每条路径最大距离50公里
  • 约束2 - 容量约束： 每条路径最多拜访35个客户
  • 约束3 - 车辆约束： 10辆小车，因此只规划10条线路

建立数据对象

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class DataProblem2():
    """Stores the data for the problem"""
    def __init__(self):
        # 可用货车数量
        self._num_vehicles = 10
        # 读取送货位置和货站位置
        df_nodes = pd.read_csv('data/deliveries.csv',sep='\s+')
        df_depots = pd.read_csv('data/stores.csv',sep='\s+')
        # 将位置存储为list
        nodes_latlon = df_nodes[['latitude', 'longitude']]
        depots_latlon = df_depots[['latitude', 'longitude']]
        # 将位置转换为tuple list
        locations = [tuple(x) for x in nodes_latlon.values]
        locations = [(tuple(depots_latlon.values[0]))]+locations
        # 定义地点对象
        self._locations = [(loc[0],loc[1]) for loc in locations]
        
        # 货站在list内的index
        self._depot = 0
        
        # 客户需求list，每个客户只送1件
        self._demands = [1]*len(locations)
    @property
    def num_vehicles(self):
        """Gets number of vehicles"""
        return self._num_vehicles
    @property
    def locations(self):
        """Gets locations"""
        return self._locations
    @property
    def num_locations(self):
        """Gets number of locations"""
        return len(self.locations)
    @property
    def depot(self):
        """Gets depot location index"""
        return self._depot
    
    @property
    def demands(self):
        """Get demand of locations"""
        return self._demands

距离

给定两点的经纬度，地表直线距离可以用Haversine公式进行计算：

$$\begin{aligned} hav(\frac{d}{r}) & = hav(lat_2 - lat_1) + cos(lat_1)\cdot cos(lat_2)\cdot hav(lon_2 - lon_1) \\ hav(\theta) &= sin^2(\frac{\theta}{2}) \\ \text{其中， }d & = 2r\cdot arcsin(\sqrt{sin^2(\frac{lat_2-lat_1}{2})+cos(lat_1)\cdot cos(lat_2)\cdot sin^2(\frac{lon_2 - lon_1}{2})}) \end{aligned}$$

其中
$(lat_1, lon_1)$和$(lat_2, lon_2)$是给定两点

$r\simeq6373 km$是地球半径

$d$是两点距离

Haversine距离计算函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def haversine_distance(position_1, position_2):
    # 地球半径(km)
    R = 6373.0
    lat1 = radians(position_1[0])
    lon1 = radians(position_1[1])
    lat2 = radians(position_2[0])
    lon2 = radians(position_2[1])
    dlon = lon2 - lon1
    dlat = lat2 - lat1
    a = sin(dlat / 2)**2 + cos(lat1) * cos(lat2) * sin(dlon / 2)**2
    c = 2 * atan2(sqrt(a), sqrt(1 - a))
    
    # 地表直线距离
    distance = R * c
    return(distance)

定义约束1 - 距离约束

Google OR tool的routing算法中，约束使用dimension对象来定义。使用.AddDimension()添加约束。 包括如下参数：

  • 约束量化表达式。在这个例子里我们定义了描述两点距离的对象distance_evaluator。对于路径规划来说，大多数约束都是基于from， to两点关系的函数。因此具有普遍性
  • slack数量。我们用0表示没有slack。
  • 最大数值上限。每条路径最大里程50公里
  • 数值初始化为0。每条路径初始里程为0
  • 约束名称。 定义好约束后，可以使用名称来调用对应的约束。在例子中，距离约束命名为“distance”， 之后使用distance_dimension = routing.GetDimensionOrDie(distance) 调用了该约束。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class CreateDistanceEvaluator(object): # pylint: disable=too-few-public-methods
    """Creates callback to return distance between points."""
    def __init__(self, data):
        """Initializes the distance matrix."""
        self._distances = {}
        # precompute distance between location to have distance callback in O(1)
        for from_node in xrange(data.num_locations):
            self._distances[from_node] = {}
            for to_node in xrange(data.num_locations):
                if from_node == to_node:
                    self._distances[from_node][to_node] = 0
                else:
                    self._distances[from_node][to_node] =(
                        haversine_distance(data.locations[from_node],
                                           data.locations[to_node]))
                                                           
    def distance_evaluator(self, from_node, to_node):
        """Returns the manhattan distance between the two nodes"""
        return self._distances[from_node][to_node]
    
    
def add_distance_dimension(routing, distance_evaluator):
    """Add Global Span constraint"""
    distance = "Distance"
    maximum_distance = 50
    routing.AddDimension(
        distance_evaluator,
        0, # null slack
        maximum_distance, # 每辆车最大路径距离50公里
        True, # 初始总距离为0
        distance)# 约束名称"distance"
    
    # 根据约束名称获取约束
    distance_dimension = routing.GetDimensionOrDie(distance)
    # 设置路径差异惩罚系数。系数越高，越倾向于用更多的车。 因为惩罚是针对车辆始末状态变化
    # 如果使用车辆，则始末状态发生变化，产生惩罚。 系数越大，惩罚越高，越倾向于少用车。
    # global_span_cost =
    #   coefficient * (Max(dimension end value) - Min(dimension start value)).
    distance_dimension.SetGlobalSpanCostCoefficient(100)

定义约束2 - 容量约束

容量约束比距离约束简单一些，每个点的货运需求均为1，不与其他点有任何的关系。即一条线路，点数量的总和不超过35。具体实现可以比照距离约束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class CreateDemandEvaluator(object): # pylint: disable=too-few-public-methods
    def __init__(self,data):
        """Initializes the demand list"""
        self._demands = data.demands
    
    # 每个点只送1件，只需要from_node即可
    def demand_evaluator(self, from_node, to_node):
        """Returns the demand for a node"""
        return self._demands[from_node]
   
def add_demand_dimension(routing, demand_evaluator):
    """Add a global capcity for each route"""
    capacity = "Capacity"
    routing.AddDimension(
        demand_evaluator,
        0,  # null slack
        35, # 线路最大客户35
        True,#  初始总容量为0
        capacity) # 约束名称"capacity"

主函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def main():
    """Entry point of the program"""
    # 建立包含原始数据的对象. 约束3-车辆约束已经在DataProblem2(）里定义了
    data = DataProblem2()
    # 建立routing模型
    routing = pywrapcp.RoutingModel(data.num_locations, data.num_vehicles, data.depot)
    # 声明距离定义函数
    distance_evaluator = CreateDistanceEvaluator(data).distance_evaluator
    # 用定义的距离作为cost
    routing.SetArcCostEvaluatorOfAllVehicles(distance_evaluator)
    # 添加约束1-距离约束
    add_distance_dimension(routing, distance_evaluator)
    # 添加约束2-容量约束
    add_demand_dimension(routing, demand_evaluator)
    # Setting first solution heuristic (cheapest addition).
    search_parameters = pywrapcp.RoutingModel.DefaultSearchParameters()
    search_parameters.first_solution_strategy = (
        routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
    # 求解
    assignment = routing.SolveWithParameters(search_parameters)
    printer = ConsolePrinter(data, routing, assignment)
    printer.print()

结果

以下是其中一辆车的结果。 共拜访14个客户，行驶10.3公里

Route for vehicle 0:
0(1) -> 190(2) -> 264(3) -> 277(4) -> 250(5) -> 241(6) -> 240(7) -> 274(8) -> 275(9) -> 12(10) -> 116(11) -> 6(12) -> 149(13) -> 290(14) -> 0
Distance of the route 0: 10.292126033856508
Load of the route: 14

最终路径如下图：

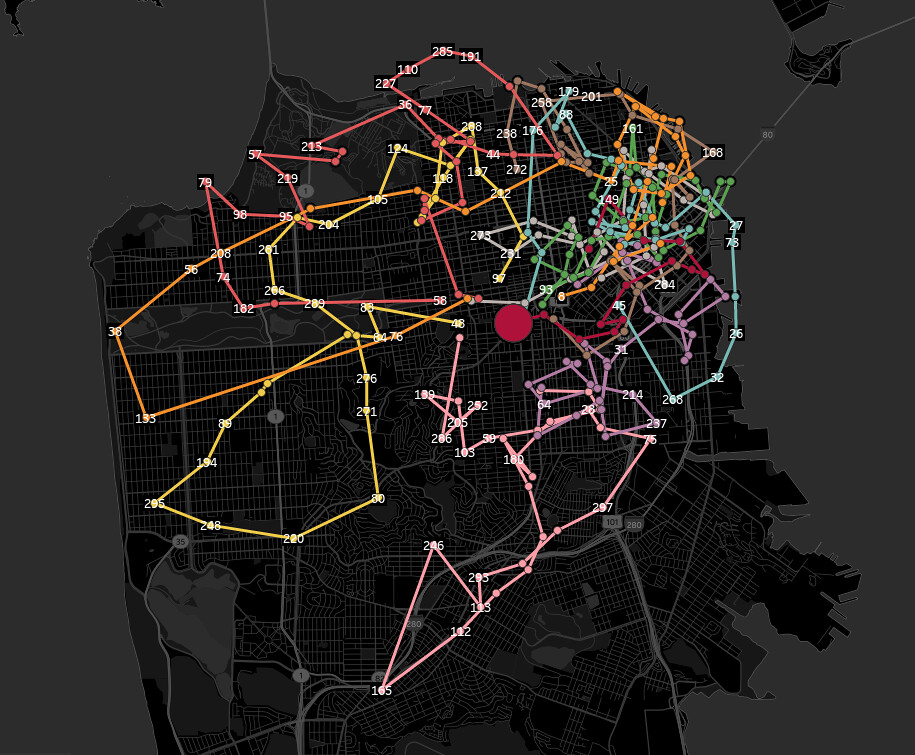
（地图使用Tableau绘制）

源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
"""Vehicle Routing Problem"""
from __future__ import print_function
from six.moves import xrange
# or-tool CP solver
from ortools.constraint_solver import pywrapcp
from ortools.constraint_solver import routing_enums_pb2
from math import sin, cos, sqrt, atan2, radians
import plotly
import googlemaps
import pandas as pd
import numpy as np
###########################
# Example of a delivery problem
###########################
class DataProblem2():
    """Stores the data for the problem"""
    def __init__(self):
        """Initializes the data for the problem"""
        self._num_vehicles = 10
        # read nodes and depots
        df_nodes = pd.read_csv('data/deliveries.csv',sep='\s+')
        df_depots = pd.read_csv('data/stores.csv',sep='\s+')
        # get lat lon info as list
        nodes_latlon = df_nodes[['latitude', 'longitude']]
        depots_latlon = df_depots[['latitude', 'longitude']]
        # creat tuple list of lat lon
        locations = [tuple(x) for x in nodes_latlon.values]
        locations = [(tuple(depots_latlon.values[0]))]+locations
        # locations in meters using the city block dimension
        self._locations = [(loc[0],loc[1]) for loc in locations]
        
        # Index of depot
        self._depot = 0
        
        # Demand per location
        self._demands = [1]*len(locations)
#######################
# Problem Constraints #
#######################
def manhattan_distance(position_1, position_2):
    """Computes the Manhattan distance between two points"""
    return (abs(position_1[0] - position_2[0]) +
            abs(position_1[1] - position_2[1]))
def haversine_distance(position_1, position_2):
    """Computes the geographical distance between two points"""
    # approximate radius of earth in km
    R = 6373.0
    lat1 = radians(position_1[0])
    lon1 = radians(position_1[1])
    lat2 = radians(position_2[0])
    lon2 = radians(position_2[1])
    dlon = lon2 - lon1
    dlat = lat2 - lat1
    a = sin(dlat / 2)**2 + cos(lat1) * cos(lat2) * sin(dlon / 2)**2
    c = 2 * atan2(sqrt(a), sqrt(1 - a))
    distance = R * c
    return(distance)
class CreateDistanceEvaluator(object): # pylint: disable=too-few-public-methods
    """Creates callback to return distance between points."""
    def __init__(self, data):
        """Initializes the distance matrix."""
        self._distances = {}
        # precompute distance between location to have distance callback in O(1)
        for from_node in xrange(data.num_locations):
            self._distances[from_node] = {}
            for to_node in xrange(data.num_locations):
                if from_node == to_node:
                    self._distances[from_node][to_node] = 0
                else:
                    self._distances[from_node][to_node] =(
                        haversine_distance(data.locations[from_node],
                                           data.locations[to_node]))
                                                           
    def distance_evaluator(self, from_node, to_node):
        """Returns the manhattan distance between the two nodes"""
        return self._distances[from_node][to_node]
    
    
class CreateDemandEvaluator(object): # pylint: disable=too-few-public-methods
    def __init__(self,data):
        """Initializes the demand list"""
        self._demands = data.demands
        
    def demand_evaluator(self, from_node, to_node):
        """Returns the demand for a node"""
        return self._demands[from_node]
def add_distance_dimension(routing, distance_evaluator):
    """Add Global Span constraint"""
    distance = "Distance"
    maximum_distance = 50
    routing.AddDimension(
        distance_evaluator,
        0, # null slack
        maximum_distance, # maximum distance per vehicle
        True, # start cumul to zero
        distance)
    # get the dimension by name
    distance_dimension = routing.GetDimensionOrDie(distance)
    # Try to minimize the max distance among vehicles.
    # /!\ It doesn't mean the standard deviation is minimized
    distance_dimension.SetGlobalSpanCostCoefficient(100)
    
def add_demand_dimension(routing, demand_evaluator):
    """Add a global capcity for each route"""
    capacity = "Capacity"
    routing.AddDimension(
        demand_evaluator,
        0,
        35,
        True,
        capacity)
###########
# Printer #
###########
class ConsolePrinter():
    """Print solution to console"""
    def __init__(self, data, routing, assignment):
        """Initializes the printer"""
        self._data = data
        self._routing = routing
        self._assignment = assignment
        self._stop = []
        self._route_num = []
        self._node_index = []
    @property
    def data(self):
        """Gets problem data"""
        return self._data
    @property
    def routing(self):
        """Gets routing model"""
        return self._routing
    @property
    def assignment(self):
        """Gets routing model"""
        return self._assignment
    @property
    def stop(self):
        return self._stop
    @property
    def route(self):
        return self._route_num
    @property
    def node(self):
        return self._node_index
    def print(self):
        """Prints assignment on console"""
        # Inspect solution.
        total_dist = 0
        for vehicle_id in xrange(self.data.num_vehicles):
            index = self.routing.Start(vehicle_id)
            plan_output = 'Route for vehicle {0}:\n'.format(vehicle_id)
            route_dist = 0
            route_load = 0
            route = []
            while not self.routing.IsEnd(index):
                node_index = self.routing.IndexToNode(index)
                next_node_index = self.routing.IndexToNode(
                    self.assignment.Value(self.routing.NextVar(index)))
                # Assign route number
                self._route_num.append(vehicle_id)
                # Assign stop number in a route
                self._stop.append(len(route))
                # Assign node index
                self._node_index.append(node_index)
                # Append node to route
                route.append(node_index)
                
                route_dist += haversine_distance(
                    self.data.locations[node_index],
                    self.data.locations[next_node_index])
                route_load += self.data.demands[node_index]
                
                plan_output += ' {node_index}({cuml_load}) -> '.format(
                    node_index=node_index, cuml_load=route_load)
                index = self.assignment.Value(self.routing.NextVar(index))
            node_index = self.routing.IndexToNode(index)
            total_dist += route_dist
            plan_output += ' {node_index}\n'.format(
                node_index=node_index)
            plan_output += 'Distance of the route {0}: {dist}\n'.format(
                vehicle_id,
                dist=route_dist)
            plan_output += 'Load of the route: {0}\n'.format(route_load)
            print(plan_output)
        print('Total Distance of all routes: {dist}'.format(dist=total_dist))
########
# Main #
########
def main():
    """Entry point of the program"""
    # Instantiate the data problem.
    data = DataProblem2()
    # Create Routing Model
    routing = pywrapcp.RoutingModel(data.num_locations, data.num_vehicles, data.depot)
    # Define weight of each edge
    distance_evaluator = CreateDistanceEvaluator(data).distance_evaluator
    demand_evaluator = CreateDemandEvaluator(data).demand_evaluator
    
    routing.SetArcCostEvaluatorOfAllVehicles(distance_evaluator)
    add_distance_dimension(routing, distance_evaluator)
    add_demand_dimension(routing, demand_evaluator)
    # Setting first solution heuristic (cheapest addition).
    search_parameters = pywrapcp.RoutingModel.DefaultSearchParameters()
    search_parameters.first_solution_strategy = (
        routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
    # Solve the problem.
    assignment = routing.SolveWithParameters(search_parameters)
    printer = ConsolePrinter(data, routing, assignment)
    printer.print()
if __name__ == '__main__':
  main()